Yingjun Mou

Yingjun Mou



I am a software engineer in a big tech company and I got my MSCS degree from Georgia Tech. My interests include computer vision, both 2D and 3D simulations, and how we can create better-structured knowledge systems to help us understand this complex world. There is more about me here. Thank you for stopping by!

Reading notes: Reasoning with latent structure refinement for document-level relation extraction

2 minute read

Published:

Reasoning with Latent Structure Refinement for Document-Level Relation Extraction

arxiv link of the source paper

1. Contributions of this paper:

1. Achieve better document-level RE/reseaoning results using a stronger graph which captures more non-local interactions. The model is called LSR(Latent Structure Refinement) model

2. This graph is treated as a latent variable, automatically induced with a refinement strategy which incrementally aggregate relevant information.

3. Example of how the model can do step-by-step “relational reasoning”:

  • Lutsenko is a former minister of internal affairs.
  • He occupied this post in the cabinets of Yulia Tymoshenko.
  • The ministry of internal affairs is the Ukranian police authority. The question is what is the relation between “Yulia Tymoshenko” and “Ukranian”. When reading the 3 sentecnes, the model will know:
    1. Lutsenko and “He” are mentions of same entity
    2. Lutsenko works with Tymenshenko
    3. Lutsenko managed internal affairs, which is a Ukranian authority
    4. Thus, Lutsenko is Ukranian -> Tymenshenko has nationality of Ukranian

2. Limitations of current practices?

1. Mostly with-in sentences, ignoring the rich information accross sentences:

  • This is because most of the current graph (even document-level) model dependencies based on (1)syntactic trees(POS), (2)coreference, or (3)heuristics
  • Do not have “relational reasoning”

3. About LSR model

1. What are the major subtasks?:

  1. Node constructor
    • (1)encode sentences with contextual representation
    • (2)construct representations of 3 types of nodes: mention, entity, and MDP(meta dependency paths)
    • What is MDP nodes?
    • In each sentences, there are multiple dependency path. The shortest parths are MDP path. The nodes in MDP paths are MDP nodes.
  2. Dynamic reasoner
    • First, it induce a doc-level structure using extracted nodes
    • Second, it keeps updateing node representations based on information propagatoin(iteratively refined)
  3. Classifier
    • Given the final node representations after refinement, calculate classification scores

2. Choice of actual model components?

  • Context enoder: BiLSTM or BERT

3. Steps

  1. Context encoding
    • Given a doc d, for sentence di, its j-th word has hidden state hij = [; ], which is the concatenation of hidden states of two directions.
    • = LSTM(, ), where is the word embedding of the j-th token.
    • Similarly, = LSTM(, )
    • In this way, the mention nodes and MDP nodes will be represented. For entity nodes, it will be constructed by averaging the related coreference mention nodes.
  2. Node extraction
    • Use tokens on shortest dependency path between mentions in sentence. It will effectively make use of relevant information while ignoring the irrelevant one.
  3. Structure induction
    • Induce latent dependency structure using structured attention and a variant of Kirchhoff’s Matrix-Tree Theorem
    • Given the representation of the i-th and j-th nodes to be ui and uj, calculate the pair-wise unnormalized attention scores sij between them. sij = (tanh(Wpui))TWb(tanh(Wcuj))
    • Compute root score which is the unnormalized probability of the i-th node to be selected as the root node of the structure sri = Wrui
    • Calculate marginal probability of each dependency edges
  4. Multi-hop reasoning
    • Use GNN, more specifically GCN(convolutional).
    • A graph G with n nodes can be represented as an n x n adjacency matrix A, which induced by previous structure induction
    • A node i at level l will have representation uli, which can be computed using ul-1i
    • Formula: 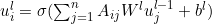![](https://latex.codecogs.com/gif.latex?\inline&space;u_{i}^{l}&space;=&space;\sigma&space;(\sum_{j=1}^n&space;A_{ij}W^lu_j^{l-1}&space;+&space;b^l%29)
  5. Iterative refinement
    • Will do refinement of structure N times, by stacking N blocks of the dynamic reasoners.
    • The induced structure will be more and more refine as more and more information aggregated
  6. Classifier
    • After N times refinements, we will get final representations of all nodes. We will compute the probability of these two entities belong to a certain relation r using a bilinear function.
    • Formula: ![](https://latex.codecogs.com/gif.latex?\inline&space;P(re_i,&space;e_j%29&space;=&space;\sigma&space;(e_i^TW_ee_j&space;+&space;b_e%29_r)